SESAmpacityBM
Finally, an accurate tool to calculate the temperature rise of Copperweld as a function of fault current characteristics!
Having a more accurate tool is important for the grounding system design engineer, who until now was left with the following perplexing sentence in Section 11.3.1 of IEEE Std. 80-2013:
Independent testing shows the actual short-term fusing currents for a copper-clad steel conductor and a copper-bonded steel ground rod can be different than those calculated by Equation (37) because of the phenomenon of variable heat capacity of steel, explained in note (d) of Table 1.
SESAmpacityBM solves this problem numerically, based on laboratory testing and published materials data, allowing the design engineer to make the most of Copperweld, which is becoming the grounding grid material of choice, due to the theft-deterrence and mechanical strength it provides, in addition to equal or better thermal and grounding performance (present-day Copperweld is also much more flexible and therefore easier to install than most people realize).
Technical Highlights
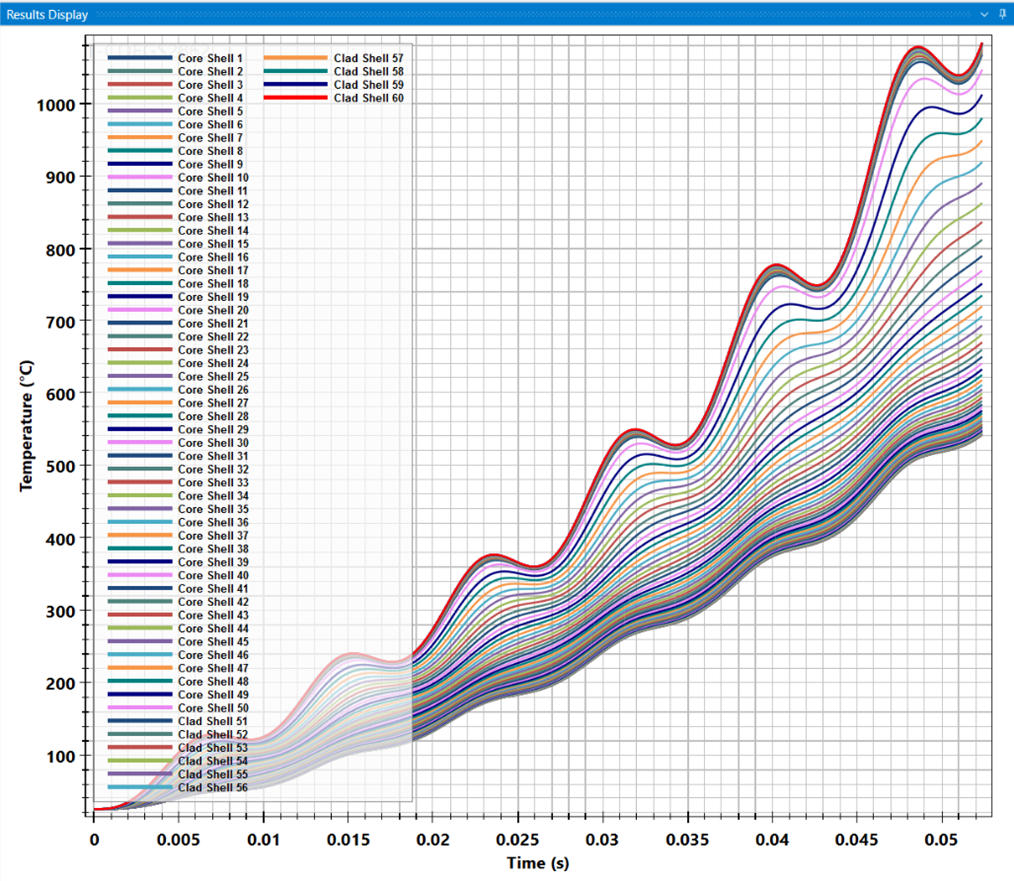
Calculating the current-carrying capacity of a bimetallic conductor can be a challenge, particularly when its steel core, unlike copper, has highly non-linear thermal characteristics, stores great amounts of heat, but is slow to transfer that heat throughout the conductor. Indeed, calculating the performance of Copperweld requires the solving of a non-linear heat transfer problem, with the copper heating up quickly and the steel core cooling it effectively… but not instantaneously. At any given time, there can be a substantial heat gradient from the copper cladding to the steel core.
SESAmpacityBM not only calculates the final temperature of a current-carrying Copperweld conductor: it also provides a graph showing you temperature distribution throughout the conductor as a function of time.
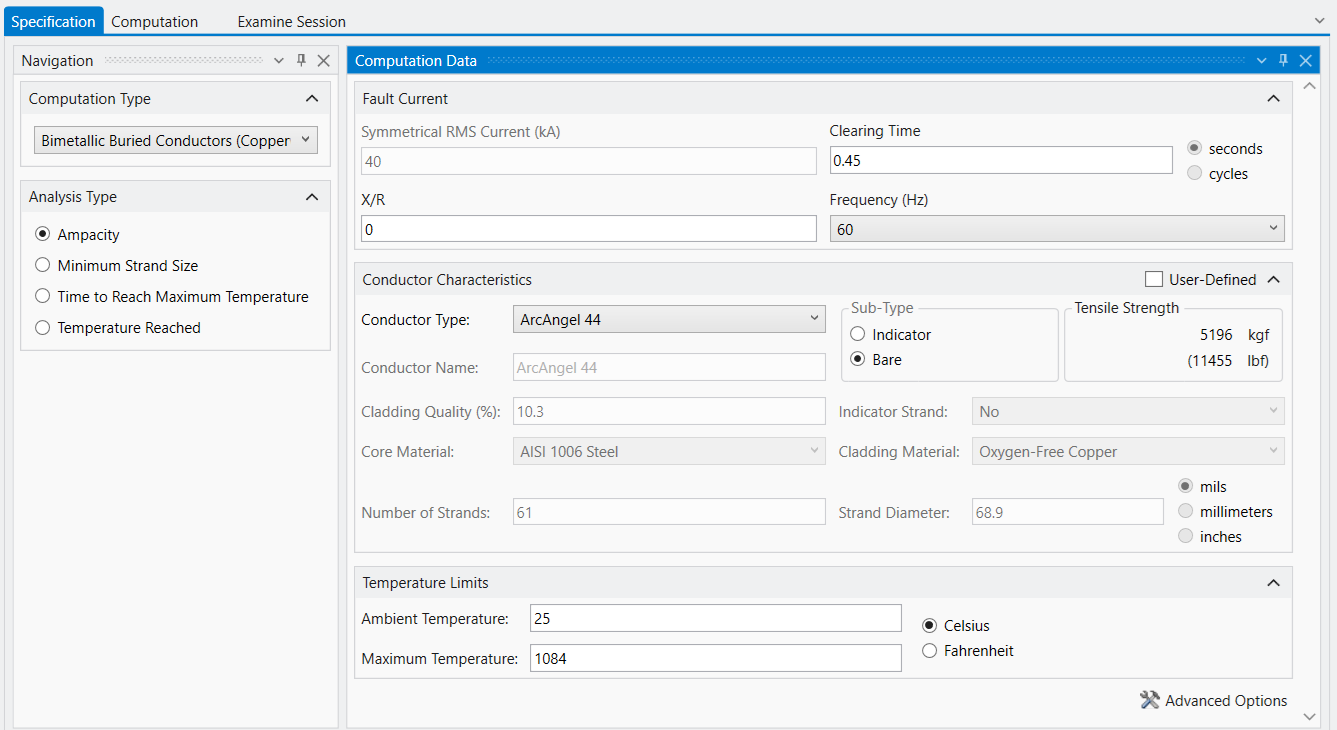
SESAmpacityBM offers the following calculations:
You can specify detailed properties of the copper-clad steel conductor, if you wish, or simply select a trade name from a drop-down menu.
Other details you can specify include system X/R ratio, power system operating frequency, ambient temperature and maximum temperature.
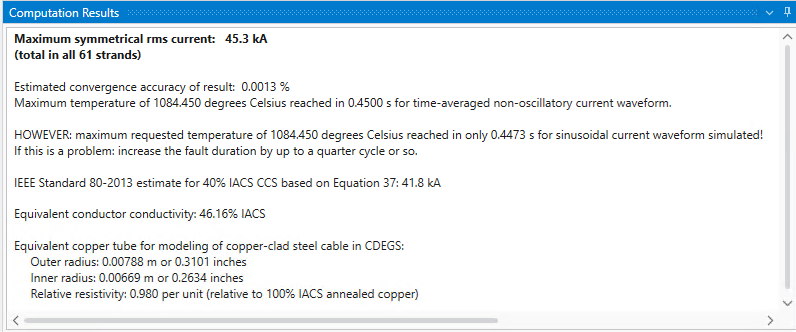
Numerical results are provided in a concise summary, which includes details on how to model the conductor in MALT, MALZ or HIFREQ:
Try it: you’ll like it!